Python查找算法之折半查找算法实现代码
本篇文章小编给大家分享一下Python查找算法之折半查找算法实现代码,文章代码介绍的很详细,小编觉得挺不错的,现在分享给大家供大家参考,有需要的小伙伴们可以来看看。
一、折半查找算法
折半查找算法又称为二分查找算法,折半查找算法是将数据分割成两等份,首先用键值(要查找的数据)与中间值进行比较。如果键值小于中间值,可确定要查找的键值在前半段;如果键值大于中间值,可确定要查找的键值在后半段。然后对前半段(后半段)进行分割,将其分成两等份,再对比键值。如此循环比较、分割,直到找到数据或者确定数据不存在为止。折半查找的缺点是只适用于已经初步排序好的数列;优点是查找速度快。
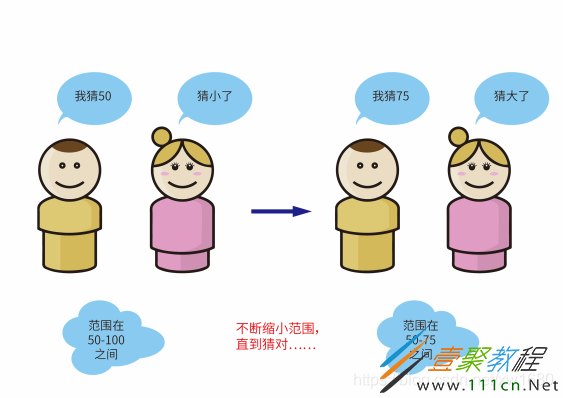
生活中也有类似于折半查找的例子,例如,猜数字游戏。在游戏开始之前,首先会给出一定的数字范围(例如0~100),并在这个范围内选择一个数字作为需要被猜的数字。然后让用户去猜,并根据用户猜的数字给出提示(如猜大了或猜小了)。用户通常的做法就是先在大范围内随意说一个数字,然后提示猜大了/猜小了,这样就缩小了猜数字的范围,慢慢地就猜到了正确的数字,如下图所示。这种做法与折半查找法类似,都是通过不断缩小数字范围来确定数字,如果每次猜的范围值都是区间的中间值,就是折半查找算法了。
例如,已经有 排序好 的数列:12、45、56、66、77、80、97、101、120,要查找的数据是 101,用折半查找步骤如下:
步骤1:将数据列出来并找到中间值 77,将 101 与 77 进行比较,如下图所示。
步骤2:将 101 与 77 进行比较,结果是 101 大于 77,说明要查找的数据在数列的右半段。此时不考虑左半段的数据,对在右半段的数据再进行分割,找中间值。这次中间值的位置在 97 和 101 之间,取 97,将 101 与 97 进行比较,如下图所示。
步骤3:将 101 与 97 进行比较,结果是 101 大于 97,说明要查找的数据在右半段数列中,此时不考虑左半段的数据,再对剩下的数列分割,找中间值,这次中间值位置是 101,将 101 与 101 进行比较,如下图所示。
步骤4:将 101 与 101 进行比较,所得结果相等,查找完成。说明:如果多次分割之后没有找到相等的值,表示这个键值没有在这个数列中。
从折半法查找的步骤来看,明显比顺序查找法的次数少,这就是折半查找法的优点:查找速度快。
二、实例:线路故障
有一条的150米线路,在这条线路上存在故障。第一天维修工已经大致锁定了几个疑似故障点,疑似故障点分别在线路的12、45、56、66、77、80、97、101、120米处。第二天维修工要在这9个疑似故障点中确定一个真正的故障点(假设真正的故障点是101米处)。维修工为了快速查找此故障点,就在每段数据的中间位置开始排查。
例如,第一次选择在77米处的疑似故障点接通电路,发现接通,他判断此故障在77米之后的位置;第二次取97米处的疑似故障点,发现也接通了,说明在97米之后的位置;第三次取101米处的位置,再次接通线路,发现未接通,说明此处是真正的故障点。此次查找经历了3次,将真正故障点找到。具体代码如下:
def search(data, num):
"""
定义查找函数:该函数使用的是折半查找算法
:param data: 原数列data
:param num: 键值num
:return:
"""
low = 0 # 定义变量用来表示低位
high = len(data) - 1 # 定义变量用来表示高位
print("正在查找.......") # 提示
while low <= high and num != -1:
mid = int((low + high) / 2) # 取中间位置
if num < data[mid]: # 判断数据是否小于中间值
# 输出位置在数列中的左半边
print(f"{num} 介于中间故障点 {low + 1}[{data[low]}] 和故障点位置 {mid + 1}[{data[mid]}] 之间,找左半边......")
high = mid - 1 # 最高位变成了中间位置减1
elif num > data[mid]: # 判断数据是否大于中间值
# 输出位置在数列中的右半边
print(f"{num} 介于中间故障点 {mid + 1}[{data[mid]}] 和故障点位置 {high + 1}[{data[high]}] 之间,找右半边......")
low = mid + 1 # 最低位变成了中间位置加1
else: # 判断数据是否等于中间值
return mid # 返回中间位置
return -1 # 自定义函数到此结束
inp_num = 0 # 定义变量,用来输入键值
num_list = [12, 45, 56, 66, 77, 80, 97, 101, 120] # 定义数列
print("疑似故障点如下:")
for index, ele in enumerate(num_list):
print(f" {index + 1}[{ele}]", end="") # 输出数列
print("")
flag = True # 开关,用来管控是否多次查找
while flag: # 循环查找
inp_num = int(input("请输入故障点:").strip()) # 输入查找键值
if inp_num == -1: # 判断键值是否是-1
break # 若为-1,跳出循环 即结束程序
result = search(num_list, inp_num) # 调用自定义的查找函数——search()函数
if result == -1: # 判断查找结果是否是-1
print(f"没有找到[{inp_num}]故障点") # 若为-1,提示没有找到值
else:
# 若不为-1,提示查找位置
print(f"在{result + 1}个位置找到[{num_list[result]}]故障点")
char = input("本次查找结束,是否继续查找,请输入 y(Y) 或 n(N):").strip()
if char.upper() == "N":
flag = False
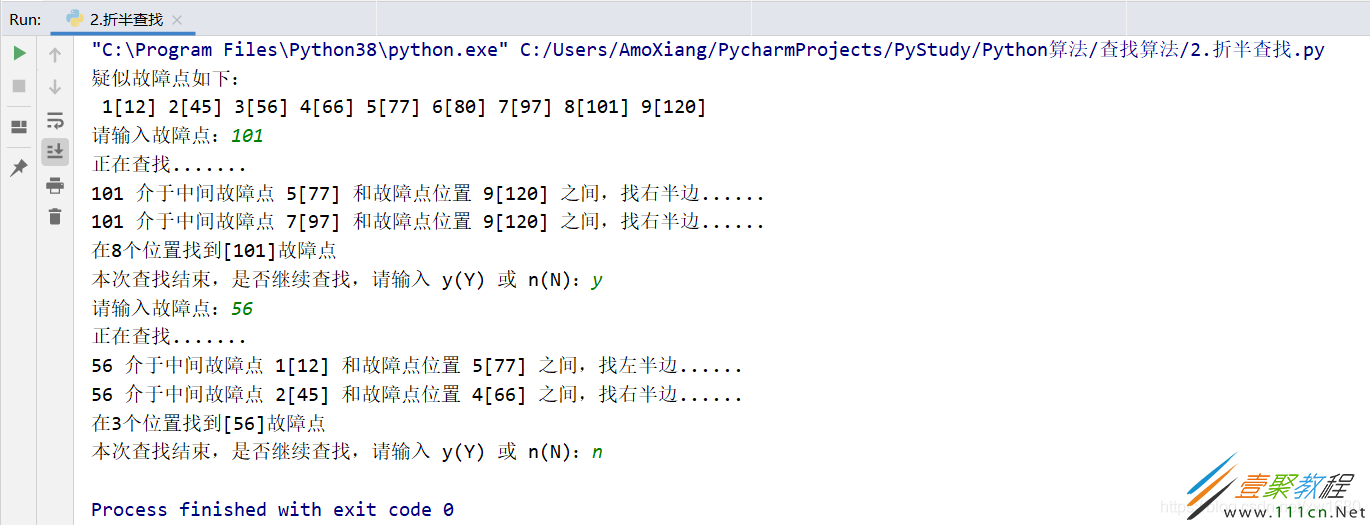
程序执行结果如下图所示: