pytorch实现线性回归以及多元回归代码示例
作者:袖梨
2022-06-25
本篇文章小编给大家分享一下pytorch实现线性回归以及多元回归代码示例,文章代码介绍的很详细,小编觉得挺不错的,现在分享给大家供大家参考,有需要的小伙伴们可以来看看。
直接附上github代码
# 实现一个线性回归
# 所有的层结构和损失函数都来自于 torch.nn
# torch.optim 是一个实现各种优化算法的包,调用的时候必须是需要优化的参数传入,这些参数都必须是Variable
x_train = np.array([[3.3],[4.4],[5.5],[6.71],[6.93],[4.168],[9.779],[6.182],[7.59],[2.167],[7.042],[10.791],[5.313],[7.997],[3.1]],dtype=np.float32)
y_train = np.array([[1.7],[2.76],[2.09],[3.19],[1.694],[1.573],[3.366],[2.596],[2.53],[1.221],[2.827],[3.465],[1.65],[2.904],[1.3]],dtype=np.float32)
# 首先我们需要将array转化成tensor,因为pytorch处理的单元是Tensor
x_train = torch.from_numpy(x_train)
y_train = torch.from_numpy(y_train)
# def a simple network
class LinearRegression(nn.Module):
def __init__(self):
super(LinearRegression,self).__init__()
self.linear = nn.Linear(1, 1) # input and output is 2_dimension
def forward(self, x):
out = self.linear(x)
return out
if torch.cuda.is_available():
model = LinearRegression().cuda()
#model = model.cuda()
else:
model = LinearRegression()
#model = model.cuda()
# 定义loss function 和 optimize func
criterion = nn.MSELoss() # 均方误差作为优化函数
optimizer = torch.optim.SGD(model.parameters(),lr=1e-3)
num_epochs = 30000
for epoch in range(num_epochs):
if torch.cuda.is_available():
inputs = Variable(x_train).cuda()
outputs = Variable(y_train).cuda()
else:
inputs = Variable(x_train)
outputs = Variable(y_train)
# forward
out = model(inputs)
loss = criterion(out,outputs)
# backword
optimizer.zero_grad() # 每次做反向传播之前都要进行归零梯度。不然梯度会累加在一起,造成不收敛的结果
loss.backward()
optimizer.step()
if (epoch +1)%20==0:
print('Epoch[{}/{}], loss: {:.6f}'.format(epoch+1,num_epochs,loss.data))
model.eval() # 将模型变成测试模式
predict = model(Variable(x_train).cuda())
predict = predict.data.cpu().numpy()
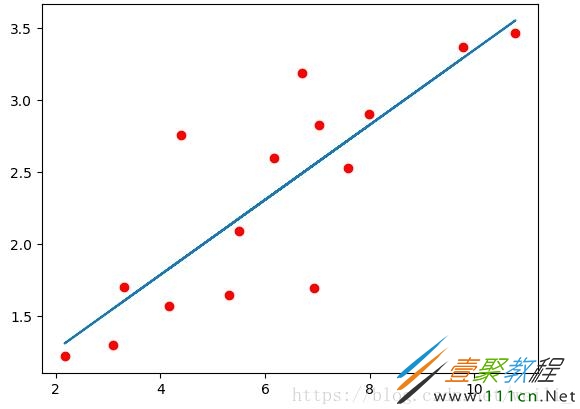
plt.plot(x_train.numpy(),y_train.numpy(),'ro',label = 'original data')
plt.plot(x_train.numpy(),predict,label = 'Fitting line')
plt.show()
结果如图所示:
多元回归:
# _*_encoding=utf-8_*_
# pytorch 里面最基本的操作对象是Tensor,pytorch 的tensor可以和numpy的ndarray相互转化。
# 实现一个线性回归
# 所有的层结构和损失函数都来自于 torch.nn
# torch.optim 是一个实现各种优化算法的包,调用的时候必须是需要优化的参数传入,这些参数都必须是Variable
# 实现 y = b + w1 *x + w2 *x**2 +w3*x**3
import os
os.environ['CUDA_DEVICE_ORDER']="PCI_BUS_ID"
os.environ['CUDA_VISIBLE_DEVICES']='0'
import torch
import numpy as np
from torch.autograd import Variable
import matplotlib.pyplot as plt
from torch import nn
# pre_processing
def make_feature(x):
x = x.unsqueeze(1) # unsquenze 是为了添加维度1的,0表示第一维度,1表示第二维度,将tensor大小由3变为(3,1)
return torch.cat([x ** i for i in range(1, 4)], 1)
# 定义好真实的数据
def f(x):
W_output = torch.Tensor([0.5, 3, 2.4]).unsqueeze(1)
b_output = torch.Tensor([0.9])
return x.mm(W_output)+b_output[0] # 外积,矩阵乘法
# 批量处理数据
def get_batch(batch_size =32):
random = torch.randn(batch_size)
x = make_feature(random)
y = f(x)
if torch.cuda.is_available():
return Variable(x).cuda(),Variable(y).cuda()
else:
return Variable(x),Variable(y)
# def model
class poly_model(nn.Module):
def __init__(self):
super(poly_model,self).__init__()
self.poly = nn.Linear(3,1)
def forward(self,input):
output = self.poly(input)
return output
if torch.cuda.is_available():
print("sdf")
model = poly_model().cuda()
else:
model = poly_model()
# 定义损失函数和优化器
criterion = nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=1e-3)
epoch = 0
while True:
batch_x, batch_y = get_batch()
#print(batch_x)
output = model(batch_x)
loss = criterion(output,batch_y)
print_loss = loss.data
optimizer.zero_grad()
loss.backward()
optimizer.step()
epoch = epoch +1
if print_loss < 1e-3:
print(print_loss)
break
model.eval()
print("Epoch = {}".format(epoch))
batch_x, batch_y = get_batch()
predict = model(batch_x)
a = predict - batch_y
y = torch.sum(a)
print('y = ',y)
predict = predict.data.cpu().numpy()
plt.plot(batch_x.cpu().numpy(),batch_y.cpu().numpy(),'ro',label = 'Original data')
plt.plot(batch_x.cpu().numpy(),predict,'b', ls='--',label = 'Fitting line')
plt.show()