利用python实现聚类分析K-means算法代码示例
作者:袖梨
2022-06-25
本篇文章小编给大家分享一下利用python实现聚类分析K-means算法代码示例,文章代码介绍的很详细,小编觉得挺不错的,现在分享给大家供大家参考,有需要的小伙伴们可以来看看。
K-means算法介绍
K-means算法是很典型的基于距离的聚类算法,采用距离作为相似性的评价指标,即认为两个对象的距离越近,其相似度就越大。该算法认为簇是由距离靠近的对象组成的,因此把得到紧凑且独立的簇作为最终目标。
算法过程如下:
1)从N个文档随机选取K个文档作为中心点;
2)对剩余的每个文档测量其到每个中心点的距离,并把它归到最近的质心的类;
3)重新计算已经得到的各个类的中心点;
4)迭代2~3步直至新的质心与原质心相等或小于指定阈值,算法结束。
算法优缺点:
优点:
原理简单
速度快
对大数据集有比较好的伸缩性
缺点:
需要指定聚类 数量K
对异常值敏感
对初始值敏感代码实现:
首先我们随机生成200个点,就取(0,2000)之间的,并确定质心个数,这里就取个3个质心,也是随机生成(可以根据需求改变)如下:
import random
import matplotlib.pyplot as plt
random_x = [random.randint(0,2000) for _ in range(200)]
random_y = [random.randint(0,2000) for _ in range(200)]
random_poinsts = [(x, y) for x, y in zip(random_x, random_y)]
def generate_random_point(min_,max_):
return random.randint(min_,max_),random.randint(min_,max_)
k1,k2,k3 = generate_random_point(-100,100),generate_random_point(-100,100),generate_random_point(-100,100)
plt.scatter(k1[0],k1[1],color = 'red',s=100)
plt.scatter(k2[0],k2[1],color = 'blue',s=100)
plt.scatter(k3[0],k3[1],color = 'green',s=100)
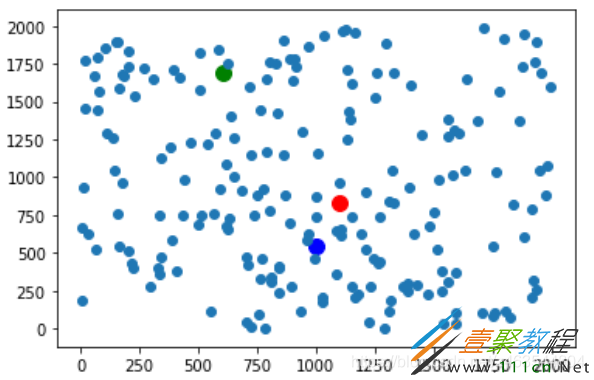
plt.scatter(random_x,random_y)
结果如下:
接着导入numpy,来计算各个点与质心的距离,并根据每个点与质心的距离分类,与第一个点近则分配在列表的第一个位置,离第二个近则分配到第二个位置,以此类推,如下
import numpy as np
def dis(p1,p2): #这里的p1,p2是一个列表[number1,number2] 距离计算
return np.sqrt((p1[0] - p2[0])**2 + (p1[1]-p2[1])**2)
random_poinsts = [(x, y) for x, y in zip(random_x, random_y)] #将100个随机点塞进列表
groups = [[],[],[]] #100个点分成三类
for p in random_poinsts: #k1,k2,k3是随机生成的三个点
distances = [dis(p,k) for k in [k1,k2,k3]]
min_index = np.argmin(distances)#取距离最近质心的下标
groups[min_index].append(p)
groups
结果如下:
[[(1000, 867),
(1308, 840),
(1999, 1598),
(1606, 1289),
(1324, 1044),
(780, 923),
(1915, 788),
(443, 980),
(687, 908),
(1763, 1039),
(1687, 1372),
(1932, 1759),
(1274, 739),
(939, 1302),
(790, 1169),
(1776, 1572),
(1637, 1042),
....
可以看到,这200个点根据与三个质心的距离远近不同,已经被分成了三类,此时groups里面有三个列表,这三个列表里分别是分配给三个质心的点的位置,接着我们将其可视化,并且加入循环来迭代以此找到相对最优的质点,代码如下:
previous_kernels = [k1,k2,k3]
circle_number = 10
for n in range(circle_number):
plt.close() #将之前的生成的图片关闭
kernel_colors = ['red','yellow','green']
new_kernels =[]
plt.scatter(previous_kernels[0][0],previous_kernels[0][1],color = kernel_colors[0],s=200)
plt.scatter(previous_kernels[1][0],previous_kernels[1][1],color = kernel_colors[1],s=200)
plt.scatter(previous_kernels[2][0],previous_kernels[2][1],color = kernel_colors[2],s=200)
groups = [[],[],[]] #100个点分成三类
for p in random_poinsts: #k1,k2,k3是随机生成的三个点
distances = [dis(p,k) for k in previous_kernels]
min_index = np.argmin(distances)#取距离最近质心的下标
groups[min_index].append(p)
print('第{}次'.format(n+1))
for i,g in enumerate(groups):
g_x = [_x for _x,_y in g]
g_y = [_y for _x,_y in g]
n_k_x,n_k_y = np.mean(g_x),np.mean(g_y)
new_kernels.append([n_k_x,n_k_y])
print('三个点之前的质心和现在的质心距离:{}'.format(dis(previous_kernels[i],[n_k_x,n_k_y])))
plt.scatter(g_x,g_y,color = kernel_colors[i])
plt.scatter(n_k_x,n_k_y,color = kernel_colors[i],alpha= 0.5,s=200)
previous_kernels = new_kernels
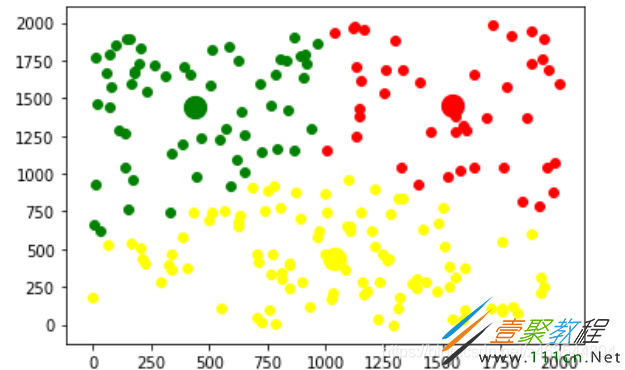
结果如下:
第1次
三个点之前的质心和现在的质心距离:344.046783724601
三个点之前的质心和现在的质心距离:178.67567512699137
三个点之前的质心和现在的质心距离:85.51258602308063
第2次
三个点之前的质心和现在的质心距离:223.75162213961798
三个点之前的质心和现在的质心距离:41.23571511332308
三个点之前的质心和现在的质心距离:132.0752155320645
第3次
三个点之前的质心和现在的质心距离:87.82012730359548
三个点之前的质心和现在的质心距离:22.289121504444285
三个点之前的质心和现在的质心距离:33.55374236991017
第4次
三个点之前的质心和现在的质心距离:50.94506045880864
三个点之前的质心和现在的质心距离:25.754704854433683
三个点之前的质心和现在的质心距离:23.145028187286528
第5次
三个点之前的质心和现在的质心距离:66.35519842692533
三个点之前的质心和现在的质心距离:31.90944410706013
三个点之前的质心和现在的质心距离:36.247409926389686
第6次
三个点之前的质心和现在的质心距离:46.17069651194525
三个点之前的质心和现在的质心距离:15.076857795406966
三个点之前的质心和现在的质心距离:42.59620276776667
第7次
三个点之前的质心和现在的质心距离:36.7751709217284
三个点之前的质心和现在的质心距离:15.873333735074496
三个点之前的质心和现在的质心距离:23.469882661161705
第8次
三个点之前的质心和现在的质心距离:0.0
三个点之前的质心和现在的质心距离:0.0
三个点之前的质心和现在的质心距离:0.0
第9次
三个点之前的质心和现在的质心距离:0.0
三个点之前的质心和现在的质心距离:0.0
三个点之前的质心和现在的质心距离:0.0
第10次
三个点之前的质心和现在的质心距离:0.0
三个点之前的质心和现在的质心距离:0.0
三个点之前的质心和现在的质心距离:0.0
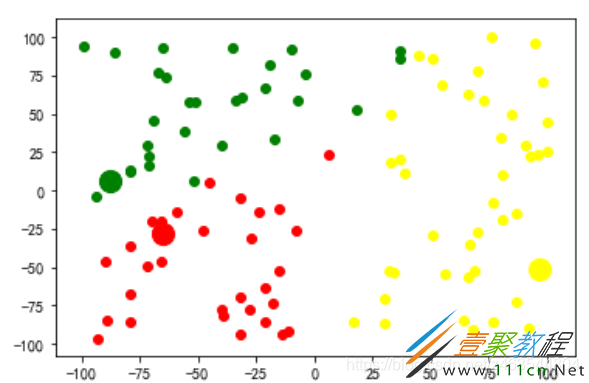
这里设置了总共迭代10次,可以看到在迭代到第八次的时候就找到了最优的质点,如图所示: