python数据可视化使用pyfinance分析证券收益代码示例解析
本篇文章小编给大家分享一下python数据可视化使用pyfinance分析证券收益代码示例解析,文章代码介绍的很详细,小编觉得挺不错的,现在分享给大家供大家参考,有需要的小伙伴们可以来看看。
pyfinance简介
在查找如何使用Python实现滚动回归时,发现一个很有用的量化金融包——pyfinance。顾名思义,pyfinance是为投资管理和证券收益分析而构建的Python分析包,主要是对面向定量金融的现有包进行补充,如pyfolio和pandas等。
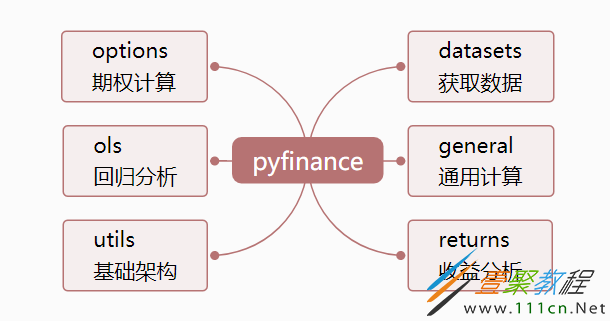
pyfinance包含六个模块
datasets.py :金融数据下载(基于request进行数据爬虫,有些数据由于外网受限已经无法下载);
general.py:通用财务计算,例如主动份额计算,收益分配近似值和跟踪误差优化;
ols.py:回归分析,支持pandas滚动窗口回归;
options.py:期权衍生品计算和策略分析;
returns.py:通过CAPM框架对财务时间序列进行统计分析,旨在模拟FactSet Research Systems和Zephyr等软件的功能,并提高了速度和灵活性;
utils.py:基础架构。
本文主要围绕returns模块,介绍pyfinance在证券投资分析中的应用,后续将逐步介绍datasets、options、ols等模块。
returns模块应用实例
pyfinance的安装比较简单,直接在cmd(或anaconda prompt)上输入"pip install pyfinance"即可。returns模块主要以TSeries类为主体(暂不支持dataframe),相当于对pandas的Series进行类扩展,使其实现更多功能,支持证券投资分析中基于CAMP(资本资产定价模型)框架的业绩评价指标计算。引用returns模块时,直接使用"from pyfinance import TSeries"即可。
下面以tushare为数据接口,先定义一个数据获取函数,在函数里对收益率数据使用TSeries进行转换,之后便可以直接使用TSeries类的相关函数。
import pandas as pd
import numpy as np
from pyfinance import TSeries
import tushare as ts
def get_data(code,start='2011-01-01',end=''):
df=ts.get_k_data(code,start,end)
df.index=pd.to_datetime(df.date)
ret=df.close/df.close.shift(1)-1
#返回TSeries序列
return TSeries(ret.dropna())
#获取中国平安数据
tss=get_data('601318')
#tss.head()
收益率计算
pyfinance的returns提供了年化收益率(anlzd_ret)、累计收益率(cuml_ret)和周期收益率(rollup)等,下面以平安银行股票为例,计算收益率指标。
#年化收益率
anl_ret=tss.anlzd_ret()
#累计收益率
cum_ret=tss.cuml_ret()
#计算周期收益率
q_ret=tss.rollup('Q')
a_ret=tss.rollup('A')
print(f'年化收益率:{anl_ret*100:.2f}%')
print(f'累计收益率:{cum_ret*100:.2f}%')
#print(f'季度收益率:{q_ret.tail().round(4)}')
#print(f'历年收益率:{a_ret.round(4)}')
输出结果:
累计收益率:205.79%
年化收益率:12.24%
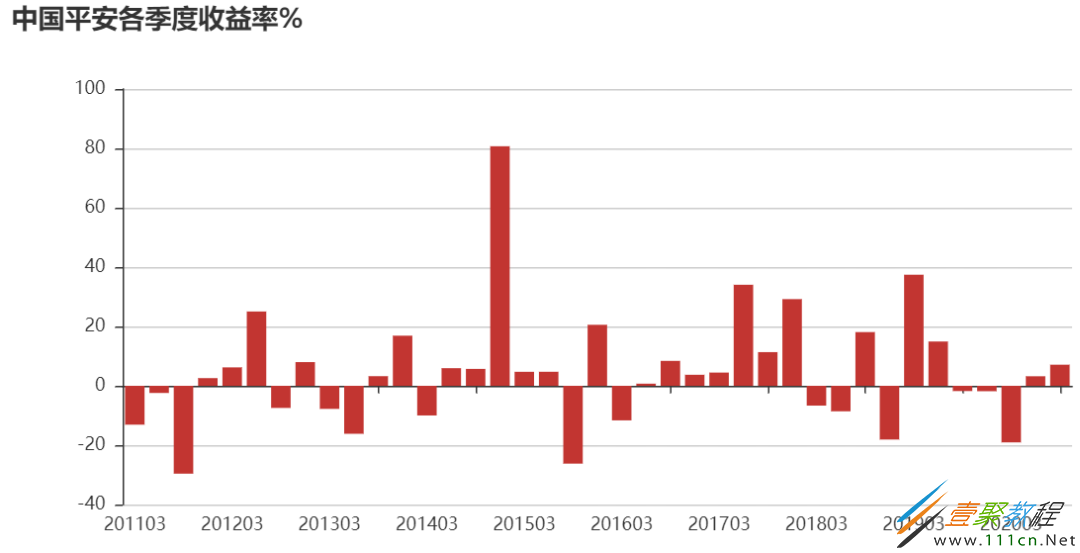
可视化每个季度(年)收益率
from pyecharts import Bar
attr=q_ret.index.strftime('%Y%m')
v1=(q_ret*100).round(2).values
bar=Bar('中国平安各季度收益率%')bar.add('',attr,v1,)
bar
from pyecharts import Bar
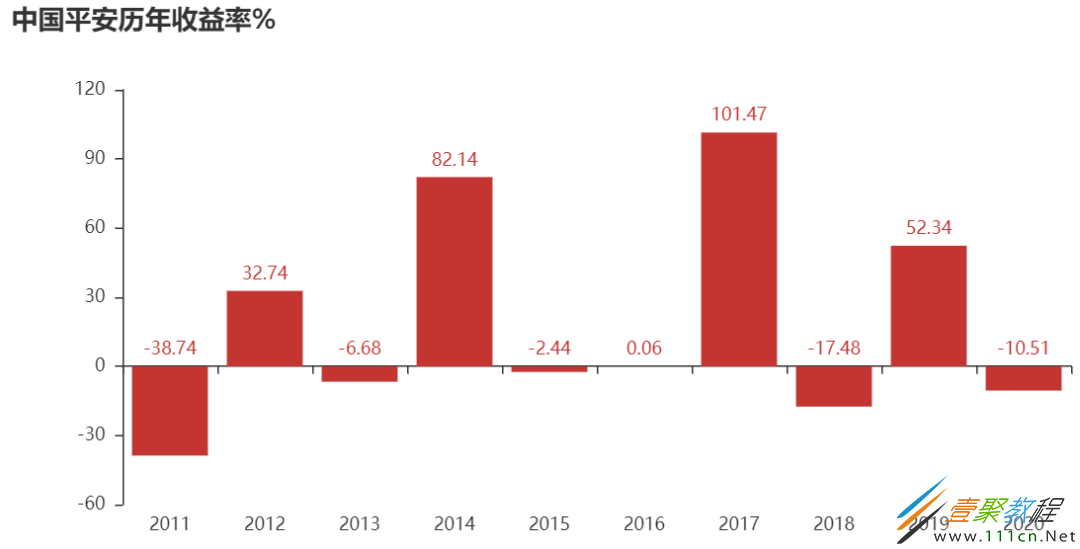
attr=a_ret.index.strftime('%Y')
v1=(a_ret*100).round(2).values
bar=Bar('中国平安历年收益率%')
bar.add('',attr,v1,is_label_show=True,
is_splitline_show=False)
bar
CAPM模型相关指标
基于CAPM模型计算alpha、beta、回归决定系数R2、t统计量和残差项等。实际上主要使用了ols回归,因此如果要获得这些动态的alpha和beta值,可以进一步借助ols模块的滚动回归函数(PandasRollingOLS)了,这将在后续推文介绍其应用。
#以沪深300指数为基准
#为保证二者长度一致,以中国平安的索引为准
benchmark=get_data('hs300')
benchmark=benchmark.loc[tss.index]
alpha,beta,rsq=tss.alpha(benchmark),tss.beta(benchmark),tss.rsq(benchmark)
tstat_a,tstat_b=tss.tstat_alpha(benchmark),tss.tstat_beta(benchmark)
print(f'alpha:{alpha:.4f},t统计量:{tstat_a:.2f}')
print(f'beta :{beta:.4f},t统计量:{tstat_b:.2f}')
print(f'回归决定系数R2:{tss.rsq(benchmark):.3f}')
alpha:0.0004,t统计量:1.55
beta :1.0634,t统计量:60.09
回归决定系数R2:0.606
风险指标
风险指标主要包括标准差和最大回撤。在计算标准差时,注意需要修改默认参数,打开pyfinance安装包所在路径,如果是安装了Anaconda,进入以下路径:
c:Anaconda3Libsite-packagespyfinance,打开returns源文件,找到anlzd_stdev和semi_stdev函数,将freq默认None改成250(一年的交易天数)。
#年化标准差
a_std=tss.anlzd_stdev()
#下行标准差
s_std=tss.semi_stdev()
#最大回撤
md=tss.max_drawdown()
print(f'年化标准差:{a_std*100:.2f}%')
print(f'下偏标准差:{s_std*100:.2f}%')
print(f'最大回撤差:{md*100:.2f}%')
年化标准差:31.37%
下偏标准差:0.43%
最大回撤差:-45.76%
下偏标准差主要是为解决收益率分布的不对称问题,当收益率函数分布左偏的情况下,使用正态分布会低估风险,因此使用传统夏普比率分母使用全样本标准差进行估计不太合适,应使用收益对无风险投资收益的偏离。
基准比较指标
基准比较指标是需要指定一个基准(benchmark),如将沪深300指数作为中国平安个股的基准进行比较分析。
bat=tss.batting_avg(benchmark)
uc=tss.up_capture(benchmark)
dc=tss.down_capture(benchmark)
tc=uc/dc
pct_neg=tss.pct_negative()
pct_pos=tss.pct_positive()
print(f'比基准收益高的时间占比:{bat*100:.2f}%')
print(f'上行期与基准收益比:{uc*100:.2f}%')
print(f'下行期与基准收益比:{dc*100:.2f}%')
print(f'上行期与下行期比:{tc*100:.2f}%')
print(f'个股下行(收益负)时间占比:{pct_neg*100:.2f}%')
print(f'个股上行(收益正)时间占比:{pct_pos*100:.2f}%')
比基准收益高的时间占比:47.83%
上行期与基准收益比:111.70%
下行期与基准收益比:105.32%
上行期与下行期比:106.06%
个股下行(收益负)时间占比:48.94%
个股上行(收益正)时间占比:50.00%
此外,信息比率和特雷诺指数是两个常用的基准比较评价指标,特别是用于对基金产品或投资组合的业绩进行量化评价。
信息比率(information ratio):以马克维茨的均值方差模型为基础,衡量超额风险所带来的超额收益,表示单位主动风险所带来的超额收益。IR=α ∕ ω (α为组合的超额收益,ω为主动风险),分子α为真实预期收益率与定价模型所计算出的收益率的差,分母为残差风险即残差项的标准差。
特雷诺指数(Treynor ratio):衡量单位风险的超额收益,计算公式为:TR=(Rp―Rf)/βp,其中:TR表示特雷诺业绩指数,Rp表示某投资组合平均收益率,Rf为平均无风险利率,βp表示某投资组合的系统风险。
ir=tss.info_ratio(benchmark)
tr=tss.treynor_ratio(benchmark)
print(f'信息比率:{ir:.3f}')
print(f'特雷诺指数:{tr:.3f}')
信息比率:0.433
特雷诺指数:0.096
风险调整收益指标
风险调整收益率指标比较常用的有夏普比率(sharpe ratio)、索提诺比率(sortino ratio)和卡玛比率(calmar ratio),这三个指标都是风险调整后收益比率,因此分子都是收益指标,分母都是风险指标。
夏普比率(Sharpe Ratio):风险调整后的收益率,计算公式:=[E(Rp)-Rf]/σp,其中E(Rp):投资组合预期报酬率,Rf:无风险利率,σp:投资组合的标准差。计算投资组合每承受一单位总风险,会产生多少的超额报酬。
索提诺比率(Sortino Ratio):与夏普比率思路一致,核心在于分母应用了下行波动率概念(Downside Risk),计算标准差的时候,不采用均值,而是一个设定的可接受最小收益率(r_min),收益率序列中,超出这个最小收益率的收益距离按照0计算,低于这个收益率的平方距离累积,这样标准差就变成了半个下行标准差。对应的,索提诺比率的分子也采用策略收益超出最低收益的部分。与夏普比率相比,索提诺比率更看重对(左)尾部的预期损失分析,而夏普比率则是对全体样本进行分析。
Calmar比率(Calmar Ratio) :描述收益和最大回撤之间的关系,计算方式为年化收益率与历史最大回撤之间的比率。Calmar比率数值越大,投资组合业绩表现越好。
sr=tss.sharpe_ratio()
sor=tss.sortino_ratio(freq=250)
cr=tss.calmar_ratio()
print(f'夏普比率:{sr:.2f}')
print(f'索提诺比率:{sor:.2f}')
print(f'卡玛比率:{cr:.2f}')
夏普比率:0.33
索提诺比率:28.35
卡玛比率:0.27
综合业绩评价指标分析实例
下面将上述常用指标进行综合,并获取多只个股进行比较分析。
def performance(code,start='2011-01-01',end=''):
tss=get_data(code,start,end)
benchmark=get_data('hs300',start,end).loc[tss.index]
dd={}
#收益率
#年化收益率
dd['年化收益率']=tss.anlzd_ret()
#累积收益率
dd['累计收益率']=tss.cuml_ret()
#alpha和beta
dd['alpha']=tss.alpha(benchmark)
dd['beta']=tss.beta(benchmark)
#风险指标
#年化标准差
dd['年化标准差']=tss.anlzd_stdev()
#下行标准差
dd['下行标准差']=tss.semi_stdev()
#最大回撤
dd['最大回撤']=tss.max_drawdown()
#信息比率和特雷诺指数
dd['信息比率']=tss.info_ratio(benchmark)
dd['特雷纳指数']=tss.treynor_ratio(benchmark)
#风险调整收益率
dd['夏普比率']=tss.sharpe_ratio()
dd['索提诺比率']=tss.sortino_ratio(freq=250)
dd['calmar比率']=tss.calmar_ratio()
df=pd.DataFrame(dd.values(),index=dd.keys()).round(4)
return df
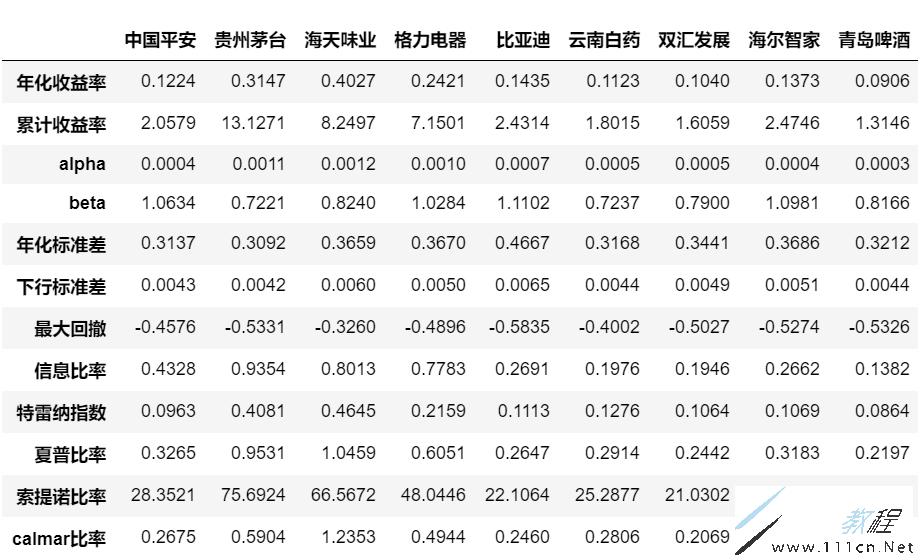
获取多只个股(也构建投资组合)数据,对比评估业绩评价指标:
#获取多只股票数据
df=pd.DataFrame(index=performance('601318').index)
stocks={'中国平安':'601318','贵州茅台':'600519',
'海天味业':'603288','格力电器':'000651',
'万科A':'00002','比亚迪':'002594',
'云南白药':'000538','双汇发展':'000895',
'海尔智家':'600690','青岛啤酒':'600600'}
for name,code in stocks.items():
try:
df[name]=performance(code).values
except:
continue
d