Python计算点到直线距离直线间交点夹角代码示例
作者:袖梨
2022-06-25
本篇文章小编给大家分享一下Python计算点到直线距离直线间交点夹角代码示例,文章代码介绍的很详细,小编觉得挺不错的,现在分享给大家供大家参考,有需要的小伙伴们可以来看看。
前言
项目中会有点到直线距离计算、两条直线交点坐标计算、两条直线夹角计算的需求。
一、点到直线距离计算
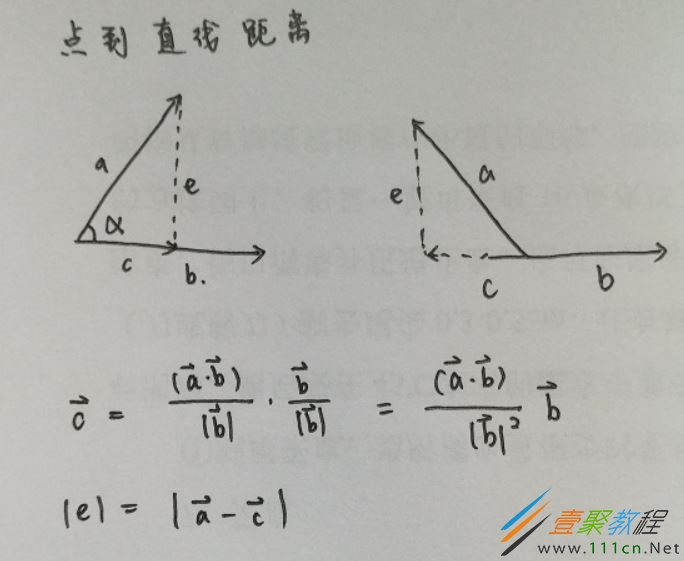
由于项目中得到点的坐标最容易,因此采用向量法进行所有的数学计算最清晰明了。点到直线距离就采用向量法推导。
import numpy as np array_longi = np.array([x2-x1, y2-y1]) array_trans = np.array([x2-line_start_x, y2-line_start_y]) # 用向量计算点到直线的举例 array_temp = (float(array_trans .dot(array_longi)) / array_longi.dot(array_longi)) array_temp = array_longi.dot(array_temp) distance = np.sqrt((array_trans - array_temp).dot(array_trans - array_temp )) # 距离
二、两条直线交点坐标计算
一般方程法:
直线的一般方程为 F(x) = ax + by + c = 0。假设直线的两个点为(x0,y0)和(x1, y1),那么可以得到 a = y0 – y1,b = x1 – x0,c = x0y1 – x1y0。
因此可以将两条直线分别表示为
F0(x) = a0*x + b0*y + c0 = 0
F1(x) = a1*x + b1*y + c1 = 0
那么两条直线的交点应该满足
a0*x + b0*y +c0 = a1*x + b1*y + c1
由此可推出
x = (b0*c1 – b1*c0) / D
y = (a1*c0 – a0*c1) / D
D = a0*b1 – a1*b0, (D为0时,表示两直线平行)
二者实际上就是连立方程组的叉积应用
F0(x) = a0*x + b0*y + c0 = 0
F1(x) = a1*x + b1*y + c1 = 0
i j k
a0 b0 c0
a1 b1 c1
class Point:
x = 0
y = 0
def __init__(self, x=0, y=0):
self.x = x
self.y = y
class Line:
def __init__(self, p1, p2):
self.p1 = p1
self.p2 = p2
def GetLinePara(line):
line.a = line.p1.y - line.p2.y
line.b = line.p2.x - line.p1.x
line.c = line.p1.x * line.p2.y - ine.p2.x * line.p1.y
def GetCrossPoint(l1, l2):
GetLinePara(l1)
GetLinePara(l2)
d = l1.a * l2.c - l2.a * l1.b
p = Point()
p.x = (l1.b * l2.c - l2.b * l1.c) * 1.0 /d
p.y = (l1.c * l2.a - l2.c * l1.a) * 1.0 /d
p1 = Point(1, 1)
p2 = Point(3, 3)
line1 = Line(p1, p2)
p3 = Point(2, 3.1)
p = Point(3.1, 2)
line2 = Line(p3, p4)
Pc = GetCrossPoint(line1, line2)
print(Pc.x, Pc.y)
三、两条直线夹角计算
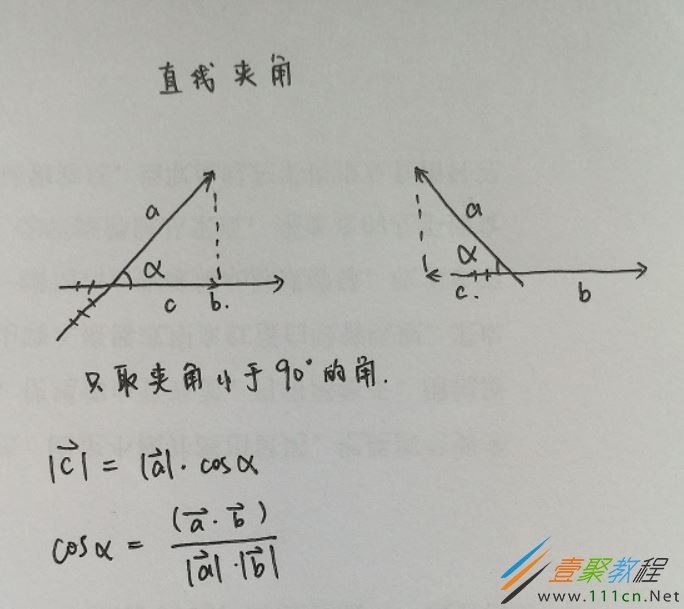
利用向量法求两条直线夹角。大致思路与求点到直线距离类似,也是利用余弦定理。
import numpy as np
def GetCrossAngle(l1, l2):
arr_0 = np.array([(l1.p2.x - l1.p1.x), (l1.p2.y - l1.p1.y)])
arr_1 = np.array([(l2.p2.x - l2.p1.x), (l2.p2.y - l2.p1.y)])
cos_value = (float(arr_0.dot(arr_1)) / (np.sqrt(arr_0.dot(arr_0)) * np.sqrt(arr_1.dot(arr_1))))
return np.arccos(cos_value) * (180 / np.pi)
angle = GetCrossAngle(line1, line2) # 计算得到的角度